
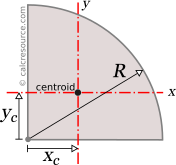
Compute the product of inertia with respect to the xy axes by dividing the section into three rectangles.Īpply the parallel axis theorem to each rectangle.9.25) and the principal moments of inertia (Eq. Determine the orientation of the principal axes (Eq.Compute the product of inertia with respect to the xyaxes by dividing the section into three rectangles and applying the parallel axis theorem to each.Mohr’s circle may be used to graphically or analytically determine the moments and product of inertia for any other rectangular axes including the principal axes and principal moments and products of inertia.įor the section shown, the moments of inertia with respect to the xand yaxes are I x= 10.38 in4and I y= 6.97 in4.ĭetermine (a) the orientation of the principal axes of the section about O,and (b) the values of the principal moments of inertia about O.The moments and product of inertia for an area are plotted as shown and used to construct Mohr’s circle,.Mohr’s Circle for Moments and Products of Inertia I max and I min are the principal moments of inertia of the area about O.
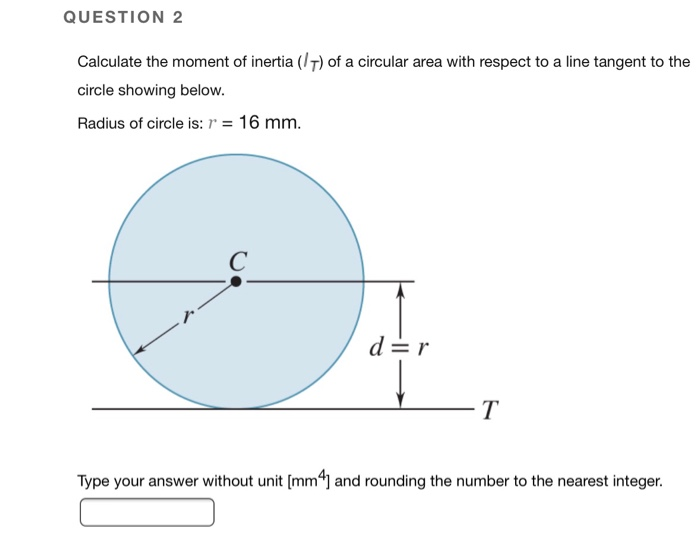
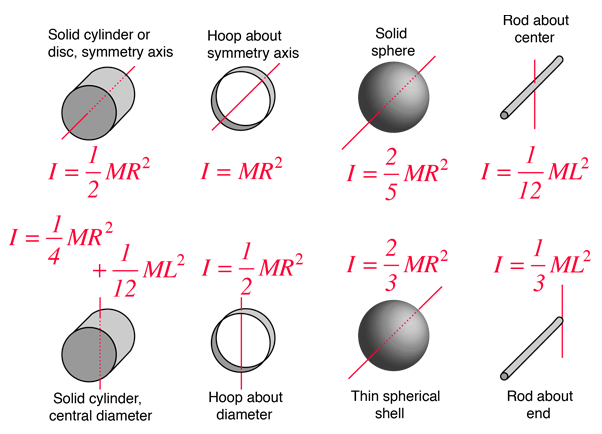
It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rotation. The moment of inertia, otherwise known as the angular mass or rotational inertia, of a rigid body is a tensor that determines the torque needed for a desired angular acceleration about a rotational axis.


 0 kommentar(er)
0 kommentar(er)
